sen(a+b) = sen a · cos b + sen b · cos a

A idéia deste segundo 'rascunho' é apresentar uma segunda maneira de deduzir fórmulas do tipo:

sen(a+b) = sen a · cos b + sen b · cos a

No primeiro 'rascunho', usamos o conceito de distância entre dois pontos (num certo sistema de coordenadas) e a definição das funções seno e cosseno no círculo de raio 1. Para o que segue, usaremos a definição do seno e do cosseno (de um ângulo) em um triângulo retângulo, e fórmula(s) para o cálculo da área de um triângulo qualquer.

:: 2ª Maneira ::

Considere o triângulo abaixo:

Sabe-se que área deste triângulo é dada por

{#} S = [z · w · sen(a+b)]/2 .

Além disso, esta mesma área também pode ser calulada por

S = (base · altura)/2

considerando a base como sendo o lado oposto ao ângulo 'a+b'. Assim, temos que

{##} S = [(x + y) · 1]/2 = (x + y)/2 .

Igualando {#} e {##}, chegamos a

[z · w · sen(a+b)]/2 = (x + y)/2

z · w · sen(a+b) = x + y

sen(a+b) = [x + y]/(z · w).

Agora, resta-nos "relacionar" as váriáveis x, y, z e w com os valores que as funções seno e cosseno assumem nos ângulos 'a' e 'b'.

|| sen a = y/w || sen b = x/z || cos a = 1/w || cos b = 1/z ||

Assim,

sen(a+b) = [x + y]/(z · w) = [x/(z · w)] + [y/(z · w)] =

[(x/z) · (1/w)] + [(1/z) · (y/w)] = [sen b · cos a] + [cos b · sen a].

E, portanto, reajustanto a última expressão teremos a igualdade desejada

sen(a+b) = sen a · cos b + sen b · cos a.

Nesta última igualdade, se trocarmos 'b' por '-b', e usarmos os fatos de cos(-b) = cos b e sen(-b) = - sen b, teremos que

sen(a - b) = sen a · cos b - sen b · cos a.

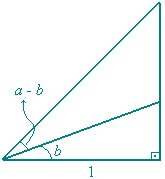
Há uma outra forma mais 'onesta' de se mostrar isto. Para tanto, pode-se utilizar a figura abaixo:

E é um bom exercício verificar tal igualdade, o qual deixaremos para o leitor!

Bibliografia

Para os dois 'rascunhos', utilizamos o livro Trigonometria Números Complexos, de autoria de Manfredo P. do Carmo, Augusto C. Morgado e Eduardo Wagner, com notas históricas de João Bosco P. de Carvalho.